From a signal processing standpoint, it is very useful to think of speech production in terms of a model, as in Figure 1. The model shown is the simplest of its kind, but it includes all the principal components. The excitations for voiced and unvoiced speech are represented by an impulse train and white noise generator, respectively. The pitch of voiced speech is controlled by the spacing between impulses, (T_p), and the amplitude (volume) of the excitation is controlled by the gain factor (G). As the acoustical excitation travels from its source (vocal cords, or a constriction), the shape of the vocal tract alters the spectral content of the signal. The most prominent effect is the formation of resonances, which intensifies the signal energy at certain frequencies (called formants). As we learned in the Digital Filter Design lab, the amplification of certain frequencies may be achieved with a linear filter by an appropriate placement of poles in the transfer function. This is why the filter in our speech model utilizes an all-pole LTI filter. A more accurate model might include a few zeros in the transfer function, but if the order of the filter is chosen appropriately, the all-pole model is sufficient. The primary reason for using the all-pole model is the distinct computational advantage in calculating the filter coefficients, as will be discussed shortly.Recall that the transfer function of an all-pole filter has the form $$V(z)=\frac{1}{1−\sum_{k=1}^{P} a_k z^−k} \qquad(1)$$, where (P) is the order of the filter. This is an IIR filter that may be implemented with a recursive difference equation. With the input (G x(n)), the speech signal (s(n)) may be written as $$ s(n)=\sum\limits_{k=1}^{P} a_k s(n−k)+G x(n) \qquad (2)$$ Speech production model

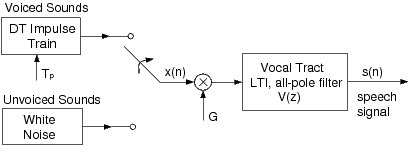
Figure 1: Impulse+noise model of speech production

Keep in mind that the filter coefficients will change continuously as the shape of the vocal tract changes, but speech segments of an appropriately small length may be approximated by a time-invariant model. This speech model is used in a variety of speech processing applications, including methods of speech recognition, speech coding for transmission, and speech synthesis. Each of these applications of the model involves dividing the speech signal into short segments, over which the filter coefficients are almost constant. For example, in speech transmission the bit rate can be significantly reduced by dividing the signal up into segments, computing and sending the model parameters for each segment (filter coefficients, gain, etc.), and re-synthesizing the signal at the receiving end, using a model similar to Figure 1. Most telephone systems use some form of this approach. Another example is speech recognition. Most recognition methods involve comparisons between short segments of the speech signals, and the filter coefficients of this model are often used in computing the “difference" between segments.

Speech Coding and Synthesis

One very effective application of LPC is the compression of speech signals. For example, an LPC vocoder (voice-coder) is a system used in many telephone systems to reduce the bit rate for the transmission of speech. This system has two overall components: an analysis section which computes signal parameters (gain, filter coefficients, etc.), and a synthesis section which reconstructs the speech signal after transmission. Since we have introduced the speech model, and the estimation of LPC coefficients, we now have all the tools necessary to implement a simple vocoder. First, in the analysis section, the original speech signal will be split into short time frames. For each frame, we will compute the signal energy, the LPC coefficients, and determine whether the segment is voiced or unvoiced.

Adapted from: Bouman, Charles A., "Lab 9b - Speech Processing (part 2)." Connexions. September 17, 2009. from http://cnx.org/content/m18087/1.3/ under the Creative Commons Attribution 2.0 Generic License.